Car Suspension System#
A car is moving over a hump in the road with a constant speed \(v \ \rm{ms^{-1}}\).
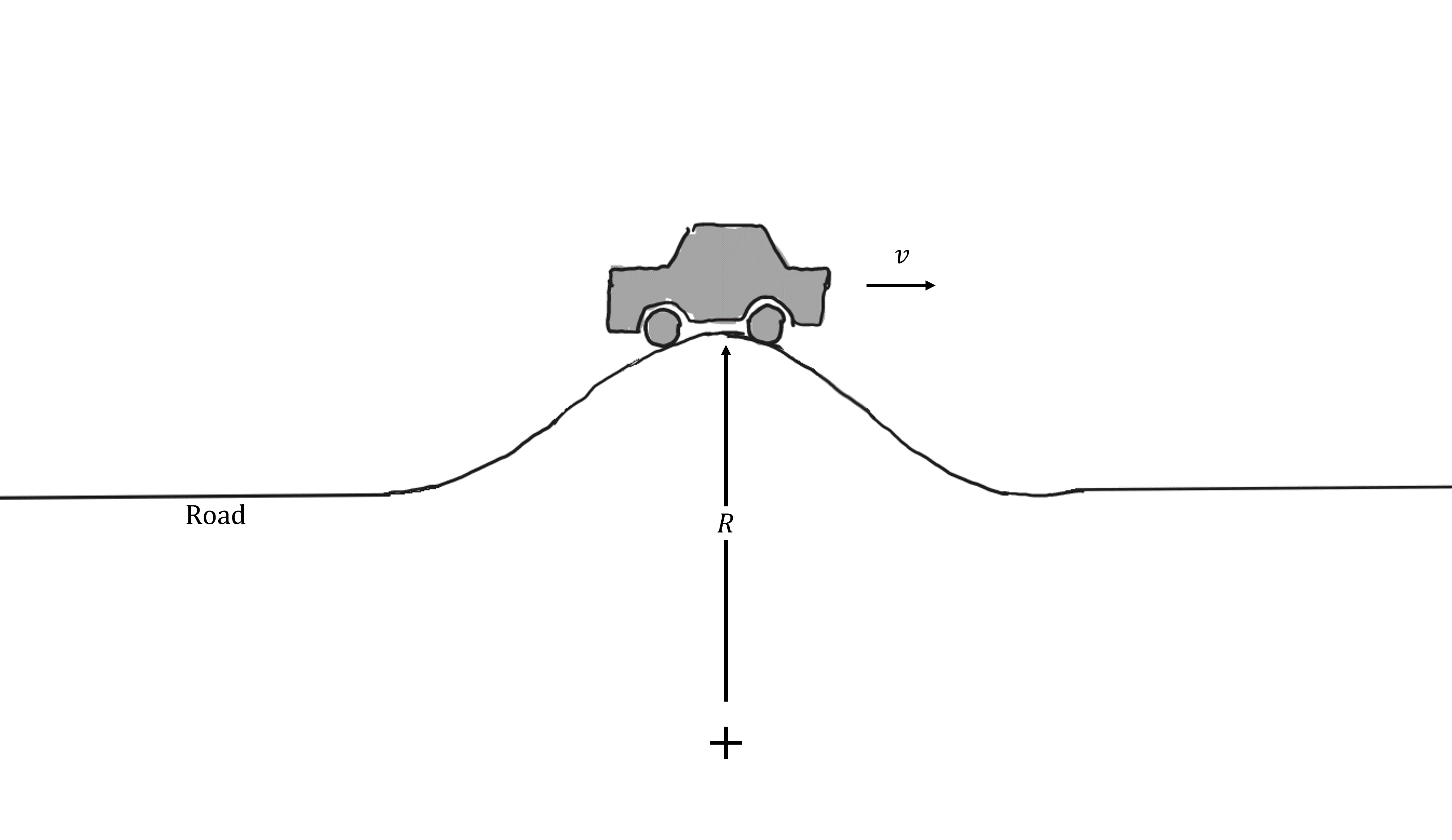
Part 1#
What is the maximum speed, \(v\) with which the car can move without it losing contact with the road at the top of the hump.
Treat the car as a particle. Neglect friction and air resistance.
\(m = {{ params.m }} \ \rm{kg}\), \(R = {{ params.r }} \ \rm{m}\)
Answer Section#
Please enter value of \(v\) in \(m/s\).
Part 2#
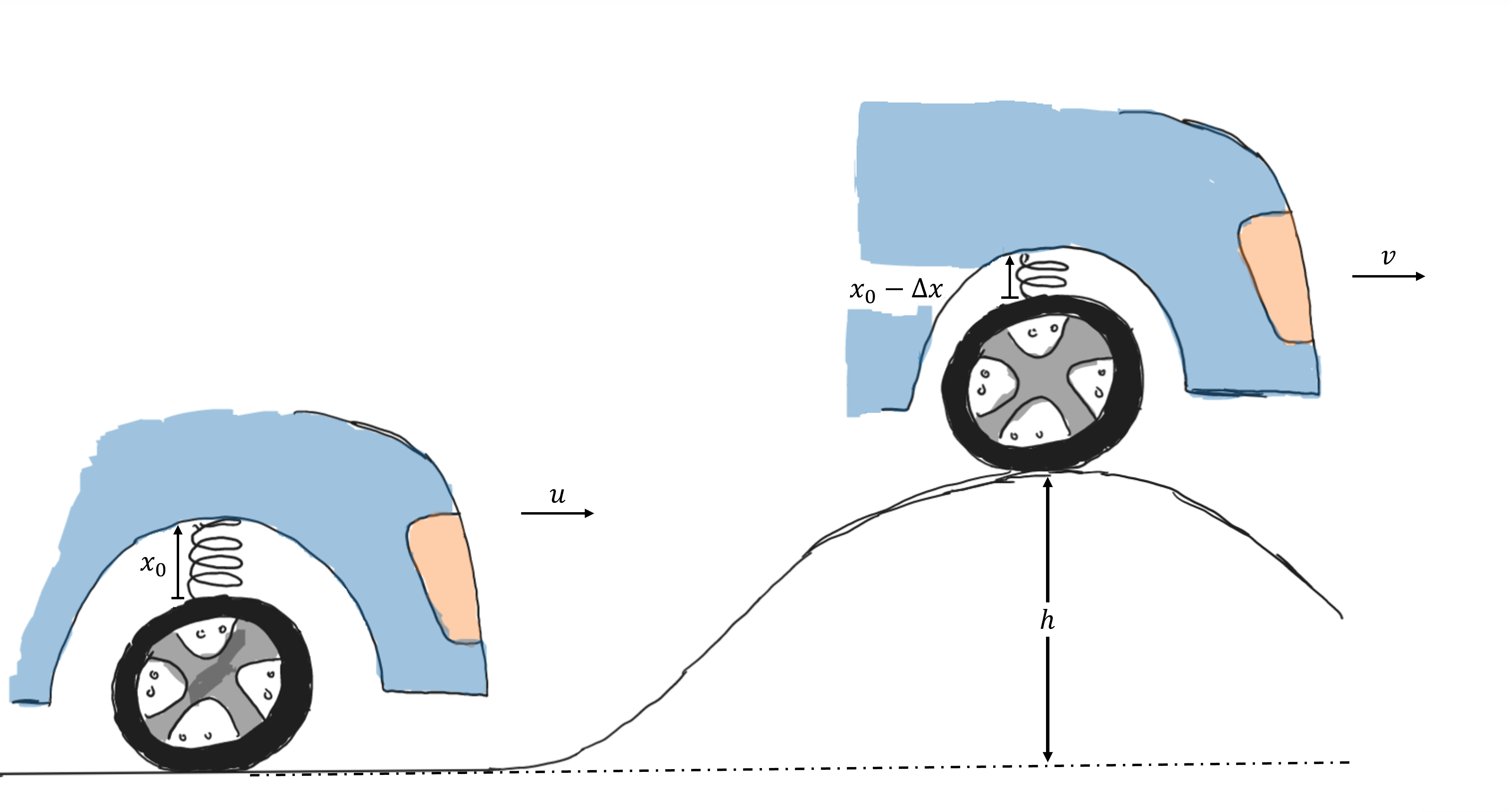
In order to reduce the likelihood of loss of contact when navigating the curvature of the hump, a suspension system consisting of a series of springs is connected to the wheels to absorb some of the excess kinetic energy of the vehicle before it encounters the circular arc.
If the maximum compression (\(\delta x\)) of the springs are \({{ params.x }}\ \rm{mm}\) at the top of the hump, what must the equivalent spring stiffness constant, \(k\), be if the speed of the car goes at the top of the hump is \({{ params.v }} \ \rm{km/h}\).
The speed of the car just before the hump is \({{ params.u }} \ \rm{km/h}\). The height of the hump above the ground plane is \(0.5 \ \rm{m}\).
Answer Section#
Please enter the value of \(k\) in \(Nm^{-1}\).
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

